
A lot of REITs talk about Weighted Average Cost of Capital, or WACC. My problem is that WACC theoretically is bad math, bad physics, and bad finance.
I know those are fighting words to many academically trained types who consider WACC “the foundation of corporate finance.” But please bear with me and I will explain.
The discussion here will apply to many other types of business. But the focus today is on REITs since that is an area I understand deeply.
Here is the basic playbook many REITs run, with details to be explained later. They look at the spread from Cap Rate to WACC and invest when it is positive, or perhaps above some threshold. Here is the relevant slide from Agree Realty (ADC), who emphasizes a threshold:
Different REITs do this differently, but for all of them it provides an empirical way to assess possible investments. It is calibrated by experience.
But conditions change (and have changed lately) and without sound theory one cannot know whether the old methods will still work. We will see below how the empirical approach can mislead.
Whence WACC?
A seminal academic paper related to economic analysis was published in 1958 by Modigliani & Miller, M&M here. (One that followed in 1961 is more often mentioned.) The work of M&M was the start of a large genre of academic publications. Our job today is not to probe the details of that genre, but to look at basics and their implications.
M&M offered their Proposition II. Proposition II speaks to the rate of return from an investment. I will do my best here to express the math in simple and conceptual form.
One key conceptual element is the rate of return on assets with no debt, which we will label Ro. For real estate properties we can recognize this as the cap rate less the costs associated with owning the property, as a fraction of property value. (For REITs is is the cap rate less associated and corporate costs.)
If we multiply this times the amount of property purchased (or equity invested), we get the absolute rate of return with no debt ($/yr). We will label this Ro X E.
This lets us express Proposition II as follows:
The absolute rate of return equals the returns from the asset without debt plus the amount of debt times the spread between Ro and interest rates. (This form is found by multiplying the usual equation by the invested equity, which makes conceptualization simpler. To get the usual form, divide through by invested equity E.)
Proposition II thus quantifies the impact of debt on returns. If next you take these steps:
Divide the above by the total property purchased (D+E),
Define the Debt Ratio as DR = D/(D+E) and note that the Equity Fraction = E/(E+D) is (1-DR),
Then you get this simplified equation:
Now this version of the Proposition is common sense. The debt both leverages up the returns and imposes interest costs.
For real estate, you can express the return on assets Ro as the cap rate less the fraction of operating earnings lost to all costs other than interest costs. If you do that, you can arrive at the formulation of three-time REIT CEO Chris Volk for ROE.
This is a straightforward, intuitively clear formulation. The unknown, ROE, is found in terms of known quantities.
You can then find the net rate of return from investments by comparing this ROE with the rate of loss of per share cash earnings associated with whatever you do to obtain that equity. If you want to issue shares, this rate of loss is the cash earnings yield. More shortly on that.
All REITs should use this analysis. But if they do, most of them keep it a secret.
Instead many REITs, and especially Net Lease REITs, rely on WACC. One way you get there is to solve Proposition II for Ro. This gives you an equation which can be viewed as a requirement on cap rate and whose right-hand side is WACC. Specifically you get:
Knowing that Ro is a bit smaller than the cap rate, you can demand that your investments have some spread to WACC (or not) and use that as a threshold for investment. Several of the net lease REITs describe their process just this way.
But there is a problem with this. ROE in Proposition II is a dependent variable. You only actually know it if you know the other variables in the equation.
What you are left with is having to somehow cook up a value for ROE in order to find WACC. There is no objective basis for this, which is why you see so many different versions advocated by different REITs or analysts.
The AFFO Yield comes in here. It is the ratio of AFFO to the Market Cap. Here AFFO is the REIT proxy for cash earnings, “Adjusted Funds From Operations.” (My preference would be so use the FAD Yield, where FAD is Funds Available for Distribution, but the present article will stay out of the weeds and stick with the traditional usage.)
One common option, which we will explore below, is to assign the AFFO Yield as the ROE in evaluating WACC. After all, the AFFO Yield is the current return on investment that market participants are getting. It is also common to use some WAG as ROE. We won’t focus on that option today, though.
The important thing is that placing a dependent variable in the role of an independent variable, as WACC calculations do, is bad math, bad physics, and therefore bad finance.
Let’s see how this plays out.
The Pieces
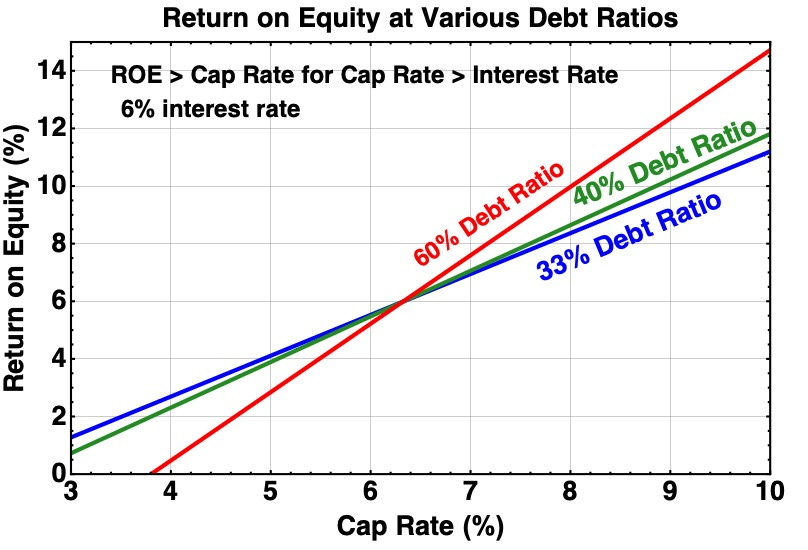
First we look at the elements of this story. Here is ROE:
When the Cap Rate exceeds the interest rate, adding leverage increases the ROE. No surprise here.
Any REIT can produce increased earnings by investing retained cash at the current ROE. Leveraging up that cash increases the earnings, for large enough cap rates.
A REIT that hopes to issue stock in order to raise equity for investment should compare ROE to the AFFO Yield. If this is positive then the investment is accretive to AFFO/sh.
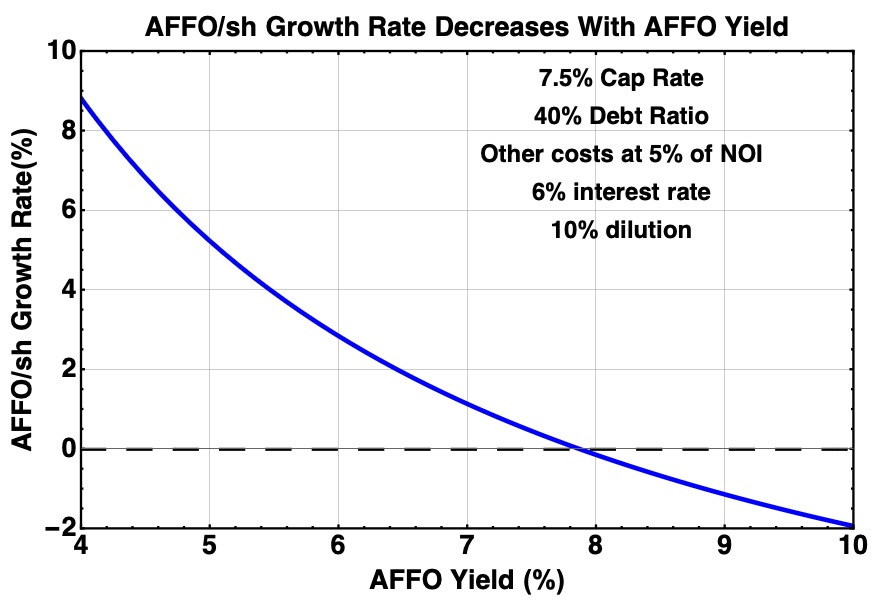
The amount of growth is proportional to the fractional net increase in AFFO times the fraction of shares issued, divided by the dilution from those shares. (This ignores internal growth, which is also diluted.) Here is how that goes for 10% dilution:
As you can see, one can find the AFFO Yield that will produce some desired threshold of AFFO/sh growth. So for these parameters to get the AFFO/sh growth produced by 10% dilution up to 2%, one would need an AFFO Yield below about 6.5%.
For reference the dividend is the payout ratio times AFFO and payout ratios to AFFO often run near 75% (but there is variation). So for this example a 4.5% dividend yield corresponds to an AFFO Yield of 6%.
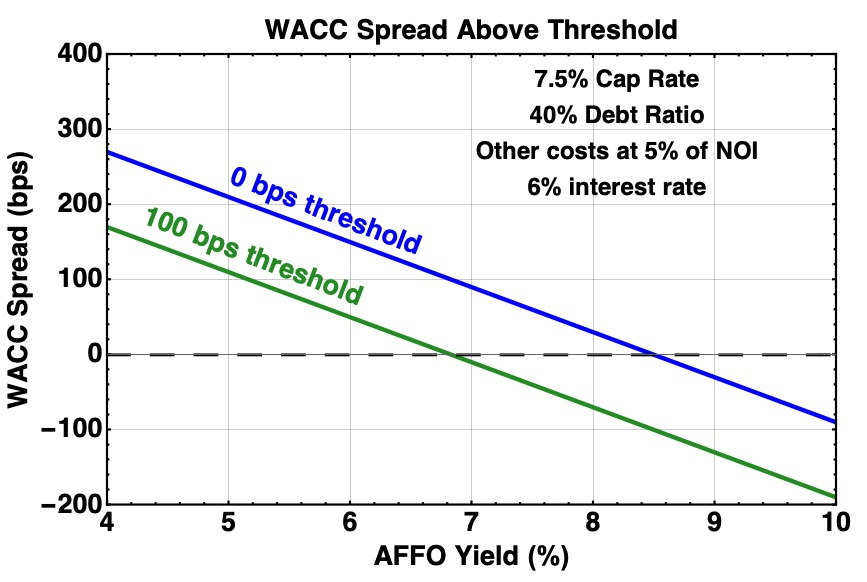
Turning to WACC, and setting the ROE in WACC to the AFFO Yield as discussed above, we can look at the WACC spread. We define WACC spread as Cap Rate minus WACC minus a threshold. (We saw above the use of thresholds by Agree Realty in considering investments.)
For the parameters used for the previous plot, we get these trends for the spread from Cap Rate to WACC:
The AFFO Yield where the spread crosses zero moves quite rapidly with the threshold. Comparing the last two plots, and doing a bunch of different cases, one finds that the threshold value of AFFO Yield for the 0 bps case is reliably above the value where the AFFO/sh growth drops below zero. In other words, investing at a 0 bps spread will lose shareholders AFFO/sh.
In contrast, using the 100 bps curve to define the investing threshold, as Agree recommends in that slide above, does consistently produce accretive investments. But these spreads do not and cannot tell you how much AFFO/sh growth you will get from an investment. This would be my major complaint about them, were they not based on bad physics.
Growth Rate at Threshold Varies
We can seek to connect the parameter REITs should care about, AFFO/sh growth with the one they say they care about, WACC spreads, as follows.
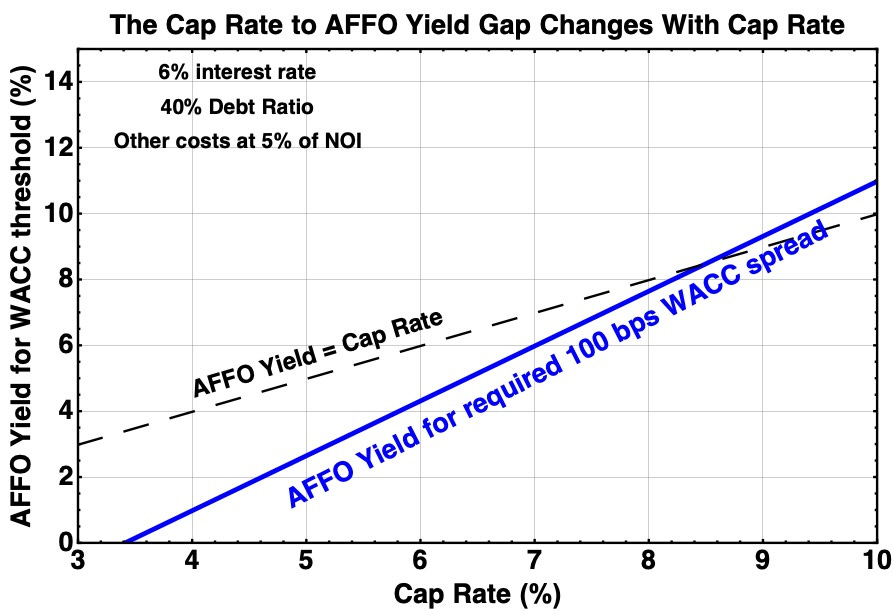
For some Cap Rate, find the AFFO Yield that puts the WACC spread at threshold. From that, calculate the AFFO/sh growth rate. Here is what you get:
This graphic captures and quantifies my main point today. You can set some WACC spread as a threshold, but as Cap Rate varies you get wildly different amounts of shareholder accretion.
To sustain a desired level of shareholder accretion, a REIT would need to push up their threshold value of WACC spread as Cap Rate increased. As best I can tell, nobody is doing that.
Even if an investment “pencils” to be accretive, it may not be worth making. Investments should add AFFO/sh accretion in proportion to their risk.
As the accretion goes down a REIT should be much more picky. But does anybody realize this? Not clear and maybe not likely.
The left side of this plot does highlight a curious aspect of REITs. The REITs with low cap rates, such as for example rental housing, produce low yields but also have produced large AFFO/sh growth.
What is going on is the consequence of this:
If you ask what AFFO yield is required to produce the threshold WACC spread, it increases with cap rate. But it also increases faster than the cap rate.
The result is that the ratio of this Cap Rate to the AFFO Yield increases at lower cap rate. This in turn produces the big increase in AFFO/sh growth we saw above.
For constant earnings multiples in the market, it is that larger AFFO/sh growth that lets those low-yield REITs compete with or even exceed the economic returns produced by higher-yield REIT sectors.
Bottom Line
My viewpoint is that REITs should seek to optimize the growth of AFFO/sh they produce. This involves a lot more than just financial numbers, in particular property quality.
But as to the numbers, WACC spreads are a very poor tool for knowing how your actions impact AFFO/sh growth. Better methods are available and are not complex to use. REITs should do so.




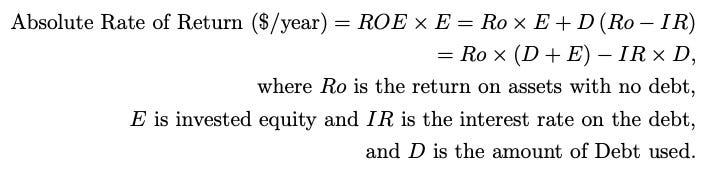
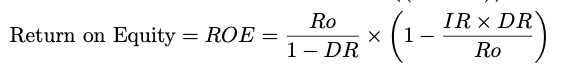
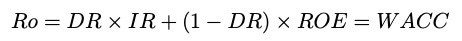

Very clever analysis. This is worth finding a way to be published on a much broader scale than Substack.
Paul having come from an environment that was focused on NAV (derived from capitalised NOI) we were always acutely aware that 25bps of compression at 4% was twice as valuable than 25bps at 8%. Taking it to the extreme, if we were at 20% yields it would be bizarre to be buying at the same spread. The lack of increased threshold / spread as acquisition yields moved up has surprised me.
That said my perspective that balances this is that RE acquired at higher cap rates will more likely see a greater % of the total return generated from compression than RE purchased at lower cap rates. (This assumes the owner trades some portion of the portfolio in some way or form). It will also benefit (typically) from higher escalation rates. The "excess rental escalation" which compounds through the long lease would provide an uplift to value which is exaggerated as yields compress.
If mathematically this sufficiently balances out the lack of additional spread sought at higher yields Im not sure.